Raining season

发表于

题面

有 $n$ 个结点的一棵树，每条边有两个权值 $a$ , $b$ ，第 $t$ 天经过第 $i$ 条边花费时间 $a_it+b$ ，给定 $m$ ，求 $t=0,1,2…m−1$ 时，最长的路径长度。

题解

这题一股浓郁的OI气息啊……（思路简单实现复杂的数据结构题）

通过分析题目，本题可以用边分治+斜率优化来解决。

简介边分治

类似点分治选择重心，边分治选择一条边，把树分成两边，使得两边的点数最接近。
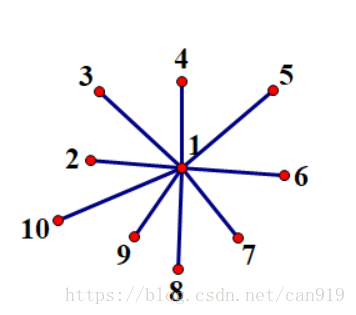
但对普通的树进行边分治容易退化，如下面这种图会退化为 $O(n)$（官方题解称为star tree）

所以使用边分治，需要将一般树，转化为二叉树，这样边分治分成的两块，保证了两块的节点数一定在 $[\frac n 3,\frac n 2]$ 之间。

边分治相对于点分治的优点在于，它只会把树分成两块，在有些情况下，合并结果时，减少大量代码量。

本题的边分治

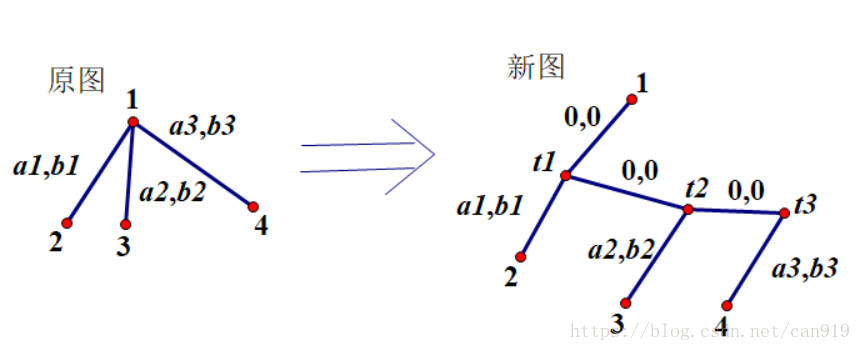
在多叉树转二叉树时，对于本题，我们必须保证任意两点的距离不变，转二叉时需要新建节点，如下图：

对于边分治的一棵数，计算每个子树的大小 siz[u] ，找到最大的子树并且大小 < 总大小的一半，选择这个结点和它父亲结点的边作为重心边，分成两棵树。

对于分成的两棵树
易知，最长路经一定是从根走到叶子节点的路径，统计所有路径，把a值和b值分别加起来，得到这条路径的函数 $at+b$ 。

这两棵树，我们都可以得到一大堆路径的函数，合并两个路径即分别相加他们的a值和b值，现在考虑如何 $O(n)$ 合并所有路径。

设 $a_i<a_j$

对于每个函数$at+b$，将其看作一个点$(a,b)$，根据斜率式，将维护上凸包，斜率递减

将分成的两棵树分别得到的所有路径函数，分别建立两个凸包。

合并时，用两个变量$x,y$，表示当前合并到这两个凸包的第几个结点，每次判断$x$与$x+1$的斜率$k1，y$与$y+1$的斜率$k2$，选择斜率更大的$+1$，再将新的$x$结点与$y$结点合并（选择斜率大的合并，保证了在新凸包中斜率变化量更小，才能使凸包中结点不漏选）

做完边分治，我们得到了整棵树所有有用路径的函数凸包，已经保证了答案的单调，直接计算即可。

代码

安利一下，代码写得很长时，变量名最好写详细一些

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
#include <bits/stdc++.h>
#define MAXN 200005
#define MAXM 600005

using namespace std;

struct Edge{
    int v,a,b,id;
    Edge()=default;
    Edge(int _v,int _a,int _b,int _id):v(_v),a(_a),b(_b),id(_id) {}
};

class Tree
{
    public:
    int n;
    vector<Edge> adj[MAXN*2];

    vector<Edge> &operator [] (unsigned int i)
    {
        return adj[i];
    }
    void AddEdge(int u,int v,int a,int b,int i)
    {
        adj[u].emplace_back(v,a,b,i);
        adj[v].emplace_back(u,a,b,i);
    }
};

struct Path
{
    long long a,b;
    Path()=default;
    Path(long long _a,long long _b):a(_a),b(_b) {}
    bool operator < (const Path &t)const
    {
        return a<t.a||(a==t.a&&b<t.b);
    }
};

int N,M,edgeid;
Tree F,G;

void ToBinaryTree(int u,int fa=0)
{
    int last=u;
    for(const auto &e:F[u])
        if(e.v!=fa)
        {
            G.AddEdge(last,++G.n,0,0,++edgeid);
            G.AddEdge(G.n,e.v,e.a,e.b,++edgeid);
            last=G.n;
            ToBinaryTree(e.v,u);
        }
}

bool disable[MAXM];
int siz[MAXN];
Edge E[MAXN];
void GetSize(int u,int fa=0)
{
    siz[u]=1;
    for(const auto &e:G[u])
        if(e.v!=fa&&!disable[e.id])
        {
            E[e.v]=Edge(u,e.a,e.b,e.id);
            GetSize(e.v,u);
            siz[u]+=siz[e.v];
        }
}
int FindCentroid(int u,int lim,int fa=0)
{
    if(siz[u]<=lim)
        return u;
    int mxsiz=0,id;
    for(const auto &e:G[u])
        if(e.v!=fa&&!disable[e.id])
        {
            int tmp=FindCentroid(e.v,lim,u);
            if(siz[tmp]>mxsiz)
                mxsiz=siz[tmp],id=tmp;
        }
    return id;
}

void GetPath(int u,vector<Path> &P,Path now=Path(0,0),int fa=0)
{
    if(G[u].size()==1)
        P.push_back(now);
    for(const auto &e:G[u])
        if(e.v!=fa&&!disable[e.id])
            GetPath(e.v,P,Path(now.a+e.a,now.b+e.b),u);
}

void Process(vector<Path> &P)
{
    static vector<Path> tmp;
    sort(P.begin(),P.end());
    tmp.resize(P.size());
    tmp.emplace_back(0,0);
    int top=0;
    for(const auto &p:P)
    {
        while(top>0&&(p.a==tmp[top].a&&p.b>=tmp[top].b))
              top--;
        if(p.a==tmp[top].a&&p.b<=tmp[top].b)
            continue;
        while(top>0&&1.0*(tmp[top].b-tmp[top-1].b)/(tmp[top].a-tmp[top-1].a)<1.0*(p.b-tmp[top].b)/(p.a-tmp[top].a))
            top--;
        tmp[++top]=p;
    }
    for(int i=0; i<=top; i++)
        P[i]=tmp[i];
    P.resize(top+1);
}

vector<Path> P1,P2,P;

void CentroidDecomposition(int u)
{
    GetSize(u);
    if(siz[u]<=1)
        return;
    int centroid1=FindCentroid(u,siz[u]/2);
    int centroid2=E[centroid1].v;

    disable[E[centroid1].id]=true;
    P1.clear();
    P2.clear();
    P1.emplace_back(0,0);
    P2.emplace_back(0,0);
    GetPath(centroid1,P1);
    GetPath(centroid2,P2);

    Process(P1);
    Process(P2);

    int x=0,y=0;
    while(x<(int)P1.size()&&y<(int)P2.size())
    {
        P.emplace_back(P1[x].a+P2[y].a+E[centroid1].a,P1[x].b+P2[y].b+E[centroid1].b);
        double k1=-1e100,k2=-1e100;
        if(x<(int)P1.size()-1)
            k1=1.0*(P1[x+1].b-P1[x].b)/(P1[x+1].a-P1[x].a);
        if(y<(int)P2.size()-1)
            k2=1.0*(P2[y+1].b-P2[y].b)/(P2[y+1].a-P2[y].a);
        if(k1>k2)
            x++;
        else
            y++;
    }

    CentroidDecomposition(centroid1);
    CentroidDecomposition(centroid2);
}

int main()
{
    scanf("%d%d",&N,&M);
    F.n=N;
    for(int i=1; i<N; i++)
    {
        int u,v,a,b;
        scanf("%d%d%d%d",&u,&v,&a,&b);
        F.AddEdge(u,v,a,b,i);
    }

    G.n=N;
    ToBinaryTree(1);

    P.emplace_back(0,0);
    CentroidDecomposition(1);
    Process(P);

    int id=0;
    for(int t=0; t<M; t++)
    {
        while(id<(int)P.size()-1&&(1LL*t*P[id+1].a+P[id+1].b)>(1LL*t*P[id].a+P[id].b))
            id++;
        long long ans=1LL*t*P[id].a+P[id].b;
        printf("%I64d ",ans);
    }
    return puts("");
}

转载自can919